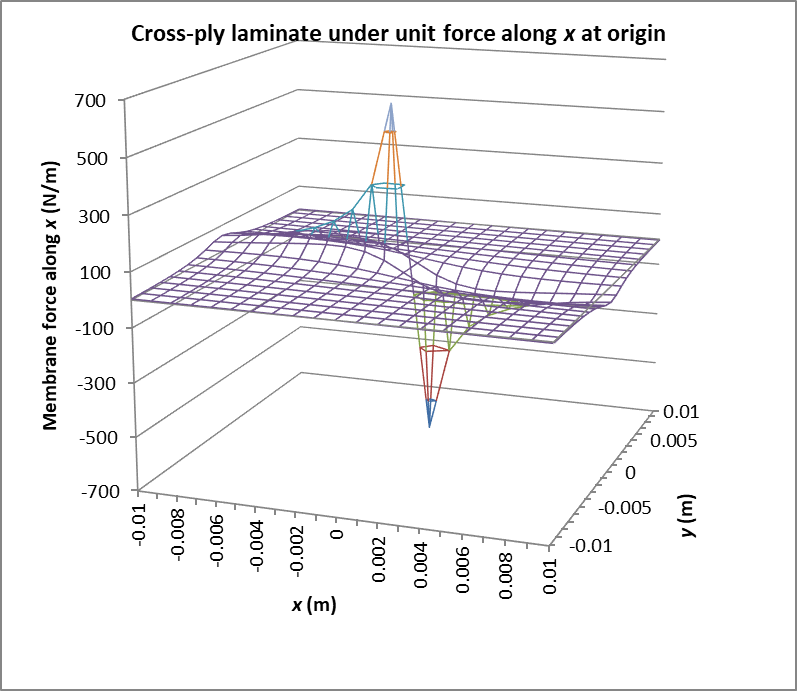
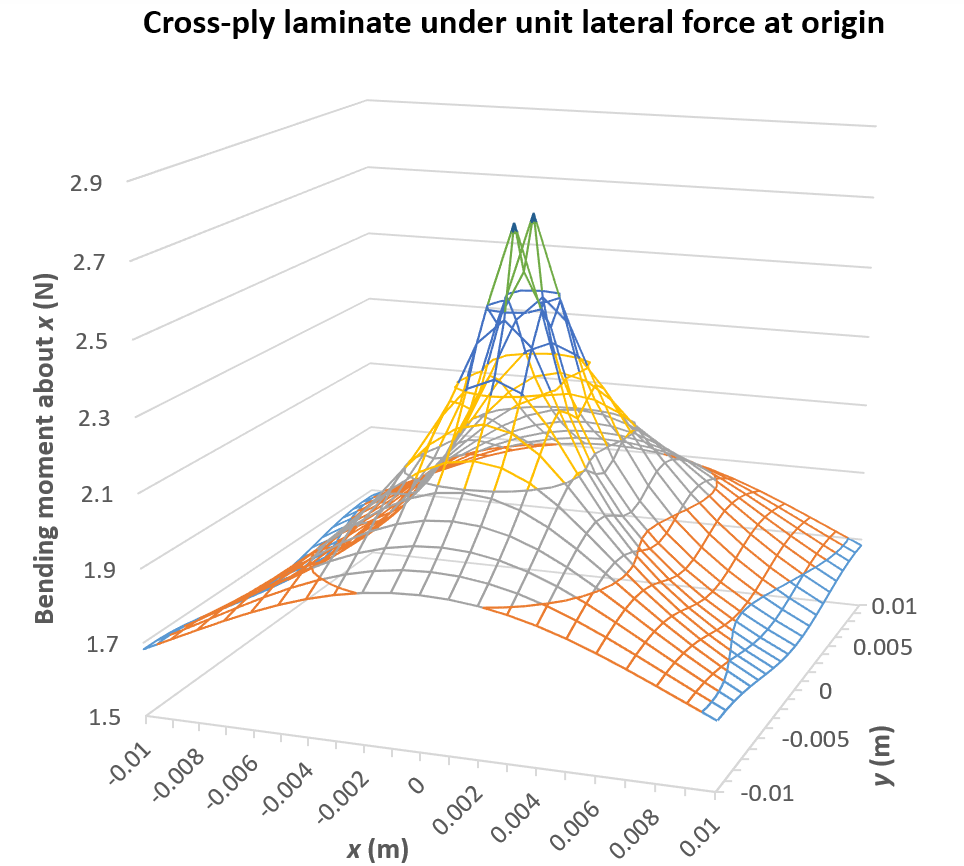
Recent theoretical work in this area resulted in closed-form analytical expressions for the fundamental solutions of the coupled extensional-flexural behaviour of asymmetrically laminated plates.
These fundamental solutions are displacements and deflections due to unit forces applied at a source point. Current work focuses on deriving expressions for the fundamental solutions for forces and moments and devising numerical schemes for the computation of all problem variables in the domain as well as along the boundary of a laminated plate. The obtained numerical results are compared with published data as a means of validating the analysis. They also confirm the validity of relations between parameters appearing in the fundamental solutions. The application of the latter to a BEM formulation for the bending of general laminates is explored addressing challenges arising in such a problem, such as the determination of the coefficients of the free term, the modelling of corner points and the evaluation of singular integrals.